This article will discuss the right triangle formula, starting from its meaning to example questions and discussion.
Hi guys ! Did you know that there are various types of triangles, one of which is a right triangle. That you know triangle with one side perpendicular to form an angle of 90 °. While the other side is slanted and that is the longest in size. How about it, have you drawn what the shape of a right triangle looks like? Instead of imagining it for too long, let’s just get into the discussion, let’s go !
What is an Right Triangle?
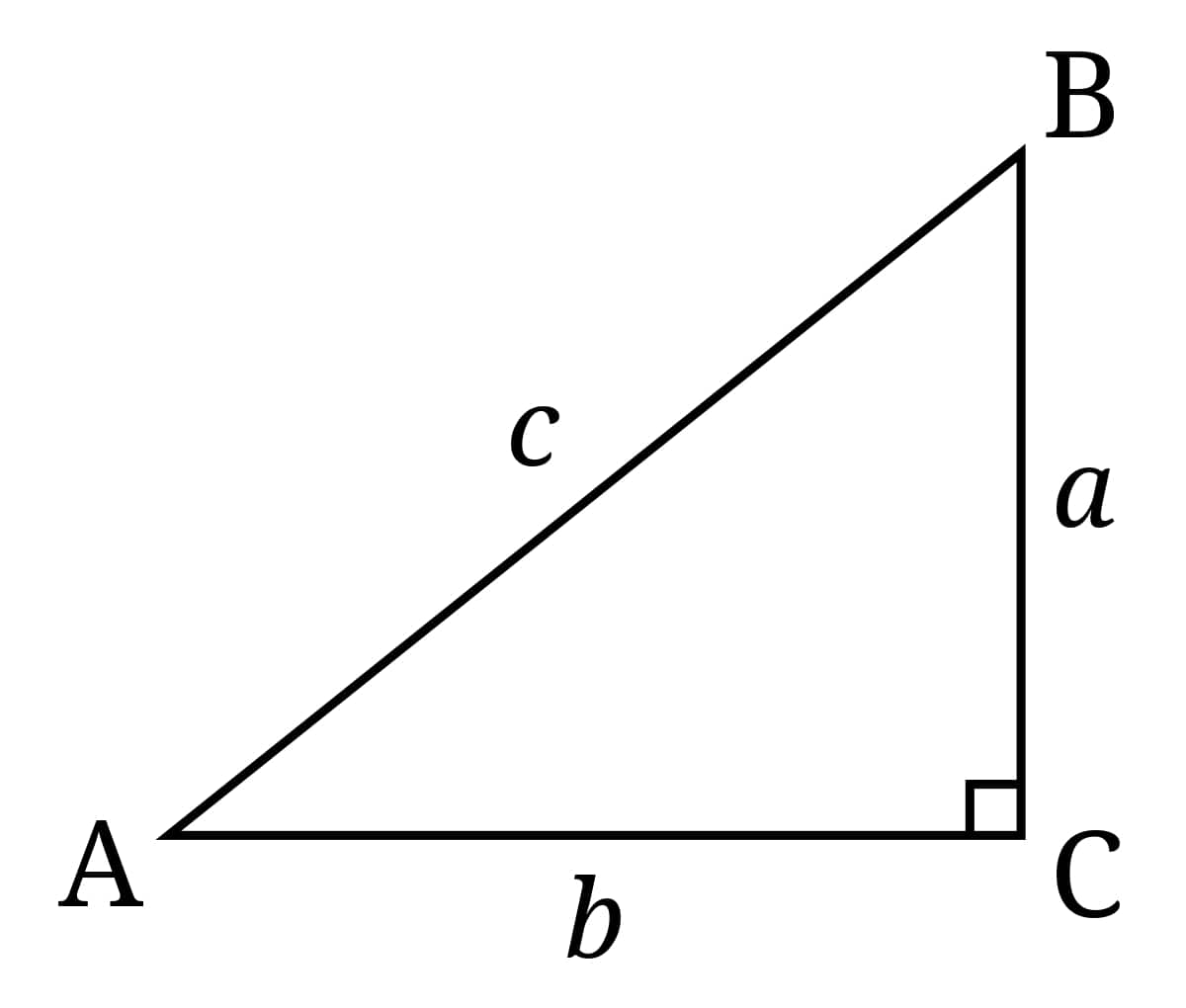
On top of already I alluded a little bit, if angled triangle is one of the triangles with one side perpendicular and form an angle of 90 °. You can see a picture of the build below:
The side c is the hypotenuse or hypotenuse. Well , the perpendicular sides are sides a and b which are called the base and height. So that you can more easily understand what the heck triangle elbow, it can be checked from the three following nature:
- A right triangle has two sides that are perpendicular to each other.
- A right triangle has one hypotenuse and one of the angles is a right angle or 90°.
- right triangles do not have rotational symmetry and folding symmetry.
Well , if you already know the three of the above properties, means already not confused anymore donk distinguish angled triangle with other triangles.
Right Triangle Formula of Area and Perimeter
After you understand the concept of a right triangle, now let’s try to calculate the circumference and area.
The perimeter of right triangle formula:
K = side a + side b + side c
The Area of right triangle formula:
L = base x height
But, what if it turns out that one of the sides of the right triangle is unknown? What formula should you use to find the length of the unknown side? Yep , how to use the Pythagorean formula. Here is the formula:
c 2 = a 2 + b 2 or c = a 2 + b 2
a 2 = c 2 – b 2 or a = c 2 – b 2
b 2 = c 2 – a 2 or b = c 2 – a 2
Sample Questions and Discussion
The formula is easy isn’t it? So , so that the formula for the circumference and the area right triangle formula for a right triangle can be easier for you to understand, also pay attention to the following examples of questions and discussions!
Example Question 1
A right triangle has sides a, b, c 3, 4, and 5, respectively. Find the perimeter of the triangle!
Discussion:
Given: a = 3; b = 4; and c = 5.
Asked: K
Answer:
K = side a + side b + side c = 3 + 4 + 5 = 12 cm
So, the perimeter of triangle ABC is 12 cm.
Example Question 2
A right triangle has a hypotenuse of 13 cm. The height of the triangle is 5 cm. Calculate the area of the triangular triangle!
Discussion:
Given: c (slope side) = 13 cm; b (height) = 5 cm.
Asked: L
Answer:
First, we must seek to know in advance how long the base of the triangle. You do this by using the Pythagorean formula.
a 2 = c 2 – b 2 = 13 2 – 5 2 = 169 – 25 = 144
a = √ 144 = 12 cm.
After knowing the base is 12 cm. Next we calculate the area.
L = x base x height = x 12 x 5 = 30 cm.
So, the area of the right triangle is 30 cm.
That’s the explanation of the area of right triangle formula. Once you know the meaning and formula, it turns out to be very easy to calculate. Hopefully the above explanation can be easily understood by you, so if you later meet a question that uses the area of right triangle formula, you will not have any difficulties.