Integer multiplication operations – From the time we enter school, we already know numbers we start to know addition and subtraction. After entering elementary school, we learn multiplication from 1 to 10. Our father or teacher at school educates us that we have to memorize multiplication from 1 to 10. After graduating from junior high school, we are required to study again or be tested again by our teacher’s father or mother. After we know and master multiplication, we will be introduced to the name number.
Of course you already know the numbers right? In this article we will talk about integers. Here’s an explanation.
Do you know what a number is? Numbers are mathematical concepts used for counting and measuring. In short, it can be said that numbers are used to represent the amount or quantity of an object.
Numbers are represented by numbers. There are groups of numbers such as integers, fractions, even numbers, odd numbers, etc. This time we will discuss operations on integers.
Definition of Integer
Traditionally, number theory was understood as a branch of pure mathematics that studies the properties of integers. It also addresses a wide range of open-ended problems that non-mathematicians can easily understand.
Reporting from coil.com numbers are built arithmetic operations as one of the operations that involve addition, subtraction, division and multiplication in the calculation of sorting numbers. Referring to this understanding, there are several types of number operations as follows.
- Addition is the combination or addition of two or more numbers to form a new number.
- Subtraction is taking a certain number from a certain number so that the number of the number is reduced.
- Multiplication is repeated addition. Multiplication can also be understood as the process of adding the same number, as many times as the multiplier.
- Division is repeated subtraction. Can also be understood as dividing a number into several groups with the same number.
In addition to the number operations mentioned above, there are also mixed types of arithmetic operations. In general, in an arithmetic operation on mixed numbers, you will find various types of arithmetic operations in one problem.
For example, questions whose solutions use addition, multiplication, subtraction, and/or division in one problem. Therefore, to calculate with mixed number operations, several things must be considered as follows.
- If the arithmetic operation includes addition and subtraction, then do the left arithmetic operation first
- If in arithmetic operations there are multiplication and division, then do the left arithmetic operations first
- If in arithmetic operations there is addition or subtraction and multiplication or division, then do the multiplication or division first
- If there are arithmetic operations in parentheses, then do the arithmetic operations in parentheses first
After knowing number theory, let’s discuss the meaning of integers. An integer is a non-fractional number consisting of
Positive integers : 1, 2, 3, 4, . . .
Zero: 0
Negative integer : . . ., -4, -3, -2, -1
In general, the set of integers is written as { . . ., -4, -3, -2, -1, 0, 1, 2, 3, 4}. Integers are denoted by Z, which comes from the word “zahlen” (German) which means number.
These integers can be written down and sorted on the number line. The use of the current number line is useful when we perform integer arithmetic operations. In integers can also be grouped into two parts viz
Even number : . . ., -6, -4, -2, 0, 2, 4, 6, . . . The even numbers are the set of numbers which, when divided by 2, gives a remainder of 0.
Odd numbers : . . ., -5, -3, -1, 1, 3, 5, . . . Odd numbers are the sets of numbers which, when divided by 2, leaves 1 or -1.
Arithmetic operations are the operations of addition, subtraction, division, multiplication, and so on. There are four types of arithmetic operations, namely multiplication, division, subtraction, and addition.
This time we will learn the multiplication operation. Multiplication is an arithmetic operation that multiplies a number by its exponent. To learn more about multiplication, pay attention to the following explanation!
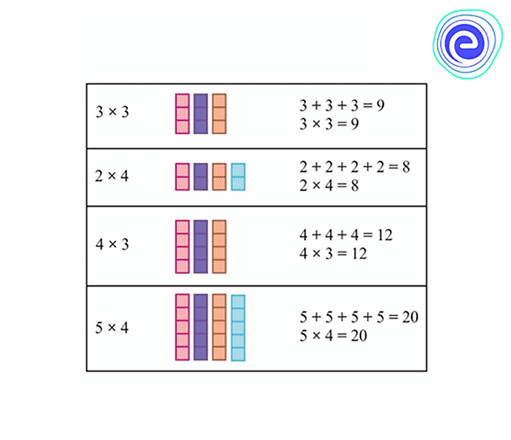
Multiplication is a form of operation on numbers which can be said to be repeated addition operations using numbers of the same size.
For more details, let’s look at the following example description…
3 x 4 = 3 + 3 + 3 + 3 = 12
4 x 3 = 4 + 4 + 4 = 12
In the multiplication example above, even though the end result is the same, the multiplication 3 x 4 and 4 x 3 have different meanings, where 3 x 4 means three times four, and for 4 x 3 it means four times three.
We can find the application of the multiplication concept in our daily life activities, such as when we go to a hospital or clinic, or health clinic. Then the doctor gives the medicine in the form of syrup, the doctor’s prescription usually says 3 x 1 on the syrup box, meaning that in a day the patient has to take 1 teaspoon of medicine three times a day in the dosage recommended by the doctor.
Doctors usually order to take medicine in the morning, afternoon and evening after eating. It’s another case if the syrup box says 1 x 3, that is, the patient is advised to drink 3 tablespoons according to the doctor’s recommendations once a day, namely in the morning, afternoon and evening.
Examples of Integers
Examples of Integers
An integer can be represented on the number line as follows.
Integer Line
In a sequence, there are integers that are grouped into parts. The integer groups are shown in the section below.
Integer Grouping
Integers are grouped into three parts, namely positive integers, zero and negative integers. In this section, we will explain positive and negative integers.
Positive Integer
The ring of positive numbers is the set of numbers consisting of 1, 2, 3, 4,. . . Positive integers are also known as natural numbers.
Negative Integer
A negative integer is the set of all numbers {. . . , -4, -3, -2, -1}. On the number line, negative integers are to the left of 0.
Next, we will approach the arithmetic operations involved in integers.
Operation Formula for Multiplication of Integers
If am and b are members of integers then:
a × b = + ( a × b )
–a × (-b) = + ( a × b )
a × (-b) = – ( a × b )
–a × b = – ( a × b )
So it can be concluded that the product of two integers can be determined based on the sign of the number in the following way:
( + ) × (+) = +
( – ) × ( – ) = +
( + ) × ( – ) = –
( – ) × (+) = –
Multiplication of Positive and Negative Integers
To find out more about multiplication of integers, both positive and negative, please refer to the following examples;
- 2 × (-7) = -14
- 3 × (-7) = -21
- 4 × (-7) = -28
- 5 × (-7) = -35
- 6 × (-7) = -42
In the example above, we can understand that the product of a positive integer and a negative integer will always produce a negative integer, so we can say “For each integer a and b, ax (-b) = – (axb) always applies.”
Multiplication of Two Negative Numbers
To be able to understand the multiplication of two negative integers, Sinaumed’s can see the following example;
- -4 x (-3) = 12
- -5 x (-2) = 10
- -7 x (-5) = 35
- -1 x (-33) = 33
- -9 x (-2) = 18
- -3 x (-3) = 9
In the example of multiplying two negative integers above, it can be concluded that the product of two negative integers will always result in a positive integer, so it can be stated “Every integer a and b always applies (-a) x (-b) = axb
Multiplication of Integers By 0 (Zero)
You can understand multiplication of integers by 0 (zero) by looking at the following example:
- 39 X 0 = 0
- 0 x -15 = 0
- -23 x 0 = 0
- 98 x 0 =0
- -11 x 0 = 0
- 0 x 346 = 0
According to the example above, it can be concluded that all numbers when multiplied by 0 (zero) will always produce 0 (zero).
Elements of Identity in Multiplication
Elements of Identity in Multiplication you can learn by looking at the following examples;
- 9 x 1 = 9
- -5 x 1 = -5
- 1 x -22 = -22
- 88 x 1 = 88
- 1 x 23 = 23
- 1 x -42 = -42
In the multiplication example above, we can conclude that any integer multiplied by 1 will produce itself. In this case, the number 1 is called the identifying factor in multiplication. so that it can be said “all integers a will always contain ax 1 = 1 xa = a
From the explanation above, it can be concluded that the operation of multiplying integers is a mathematical operation that involves the sign “x”. Multiplication is also known as repeated addition.
The properties of the multiplication operation are described in the following sections.
axb = ab : the product of two positive integers is a positive integer.
Example: 5 x 6 = 30. 5, 6, 30 are positive integers.
ax (-b) = -ab : the result of multiplying a positive integer by a negative integer results in a negative integer.
Example: 3 x (-4) = -12. The result of the operation is -12 (negative integer).
(-a) x (-b )= ab : the product of two negative integers is a positive integer.
Example: (-5) x (-2) = 10, resulting in a positive integer that is 10.
Properties of Multiplication in Integers
1. Closed Nature
The closed property is one of the properties of the integer addition operation, where this property can also be found in the multiplication operation. In multiplication, the closure property means that any multiplication of integers always results in an integer. It can be stated as “For any integers p and q, there will always be pxq = r, where r is also an integer”.
For more details about the closing properties of integer multiplication, you can see the sample questions below:
4 x 3 = 12
where 4 and 3 we know are integers, as well as 12 which is also an integer.
5 x (-4) = -20
where 5 and -4 we know are integers, and so is -20 which is also an integer.
-7 x 2 = -14
where -7 and 2 we know are integers, as well as -14 which is also an integer.
-6 x (-4) = 24
where -6 and -4 we know are integers, as well as 24 which is also an integer.
2. Commutative Nature (Exchange)
The commutative property (exchange) in the multiplication operation is that multiplication will always receive the same output even if the two numbers are swapped. So that this can be written “For every sapta p & q will always apply pxq = qxp”.
For details about the commutative property in the multiplication operation, you can see the problem model below:
6 x (-4) = (-4) x 6 =-24
(-5) x (-8) = (-8) x (-5) = 40
3. Associative nature (grouping)
In this property, it is expressed as “For every number p, and q and r, will always hold ( pxq ) xr = px ( qxr)”.
To make it easier for sinaumedia friends to understand the associative nature (grouping) of integer multiplication operations, take a look at the following example questions;
problems example;
3 x (-5 x 2) = ( 3 x (-5) ) x 2 = -30
( -4 x 6 ) x 3 = -4 x ( 6 x 3) = -72
4. Distributive Properties of Multiplication Against Addition
In this property it is stated that “For every number p, q, and r which are integers, it will always apply
px (q + r) = (pxq) + (pxr)”.
For more details about the distributive property of multiplication over addition in the multiplication operation of integers, you can refer to the description of the problem below;
problems example;
4 x ( 5 + (-3) ) = 4 x 2 = 8
can also be solved by, ( 4 x 5) + ( 4 x (-3) ) = 20 + (-12) = 8
so, 4 x ( 5 + (-3) ) = ( 4 x 5) + ( 4 x (-3) ) = 8
(- 5) x ( -3 + 6) = (-5) x 3 = -15
can also be solved by, ( (-5) x (-3) ) + ( (-5) x 6 ) = 15 + (-30) = -15
so, (- 5) x ( -3 + 6) = ( (-5) x (-3) ) + ( (-5) x 6 ) = -15
5. Distributive Properties of Multiplication Against Subtraction
This property is expressed as “For every p, q, and r which are integers, will always apply
px ( q – r ) = (pxq) – ( pxr) “.
For more details about the Distributive Property of Multiplication Against Subtraction in the multiplication operation of integers, you can refer to the description of the problem below;
problems example;
3 x ( 7 – (-6) ) = 3 x 13 = 39
can also be solved by, (3 x 7) – (3 x (-6) ) = 21 – (-18) = 21 +18 = 39
so, 3 x ( 7 – (-6) ) = (3 x 7) – (3 x (-6) ) = 39
5 x ( -4 – 2) = 5 x (-6) = -30
can also be solved by, (5 x (-4) ) – (5 x 2) ) = -20 – 10 = -30
so, 5 x ( -4 – 2) = (5 x (-4) ) – (5 x 2) ) = -30
6. Has an Element of Identity
The number 1 is the identity element in multiplication. This means that any integer when multiplied by the number 1 will produce the number itself.
this can be stated by “For every number p which is an integer, it will always apply px 1 = 1 xp = p”.
for example;
13 x1 = 13 or 1 x 13 = 13
34 x 1 = 34 or 1 x 34 =34
Problems example
Examples of Positive Number Multiplication Operation Problems
1.(+12)x(+5)
(+4) x (+40)
Discussion:
Multiplication of positive numbers is calculated the same as when we multiply numbers in general.
(+12) x (+5) = 12 x 5 = 60
(+4) x (+40) = 4 x 40 = 160
2. Topic received a donation of 8 sacks of rice. Each sack weighs 85 kg. The rice was distributed to 17 employees. Each employee gets as much rice as…
- 18 kgs
- 24 kgs
- 36 kgs
- 40 kgs
The answer to the multiplication of the total integer number of rice received by Topik is…
8 x 85 kg = 680 kg
Each employee gets 680 kg of rice: 17 = 40 kg
Answer: D
3. Tony sent letters to 3 of his friends. 2 pieces of letter wearing stamps worth @ 500 and a letter wearing a postage of Rp. 250. So, the amount of money needed to buy the stamps is..
- 1,000
- 1,250
- 1,500
- 1,750
Answer:
The amount of money needed to buy stamps is
=(2 x 500) + (1 x 250)
= 1,000 + 250
= 1,250
Answer: B
4. Calculate the multiplication operation of this positive number with associative property
9 x (13 x 2)
(20 x 36) x 3
Discussion:
Enter the formula for calculating multiplication of integers with associative properties first.
(axb) xc = ax (bxc) = d
Then, enter the multiplied numbers in the problem according to the associative property formula.
9 x (13 x 2)
(axb) xc = ax (bxc) = d
9 x (13 x 2) = (9 x 13) x 2 = 117 x 2 = 234
(20 x 36) x 3
(20 x 36) x 3 = 20 x (36 x 2) = 20 x 72 = 1440
Examples of Problems with Multiplication of Negative Numbers
1.(-6) x (-12)
(-4) x (-23)
Or more concisely, the multiplication result between numbers with the same sign produces a positive number.
The calculation method is quoted from the Mathematics book for Middle School Class VII of the Freedom Learning Curriculum.
(-6) x (-12) = 72
(-4) x (-23) = 92
Examples of Operational Problems Adding Positive and Negative Numbers
1.(-80) x (+15)
(-5) x (+56)
Discussion:
Based on the Mathematics book for Class VII Middle School Independent Learning Curriculum, the product of numbers with different signs produces a negative number.
(-80) x (+15) = -1200
(-5) x (+56) = -280
2. ((-80) x 15) x 4)
(-2) x ((-5) x 56)
Discussion:
((-80) x 15) x 4) = (-80) x (15 x 4) = (-80) x 60 = -4800
(-2) x ((-5) x 56) = ((-2) x (-5)) x 56 = 10 x 56 = 560
3. The result of the number operation from 7 x (-13) is ….
- A.91
- B. -20
- C.20
- D. 91
Discussion:
7 x (-13) = ….
7 is positively charged while
(-3) is negatively charged
Multiplying a positive number by a negative number will result in a negative number, so it becomes:
7 x (-13) = – (7 x 13)
= -91
4. 19. -11 x 8 ….. (-8) x 11
The appropriate comparison sign to complete the statement above is ….
- <
- >
- =
- ≥
Discussion:
-11 x 8 = (-88) whereas
(-8) x 11 = (-88)
Then -11 x 8 and (-8) x 11 result in the same number. So the exact comparison sign is equal to or (=).
Closing
That’s all Sinaumed’s friends , a little explanation about multiplication on integers that we can convey, sorry if there are errors in writing and calculations.